ssidfilehipo

                                             බබිලෝනියානු ගණන් කථාව

ස්කැන්කර් වගුව (ප්ලේට් 18). බබිලෝනීය ගණිතයේ බුදුරජාණන් වහන්සේ විසින් ලියන ලද බුදුරජාණන් වහන්සේ විසින් ලියන ලද ලියවිල්ලක් මෙහි දැක්වේ. මෙම වගුවේ වගුව සමඟ Base 60 භාවිතා කළ හැකි ආකාරය දැක ගත හැකිය. http://www.gutenberg.org/files/16161/16161-h/16161-h.htm - මහා රාජාණ්ඩු හීන්, ජී. රාවින්සන්

අපගේ අංකවලින් වෙනස් වූ ප්රධාන කොටස් තුන

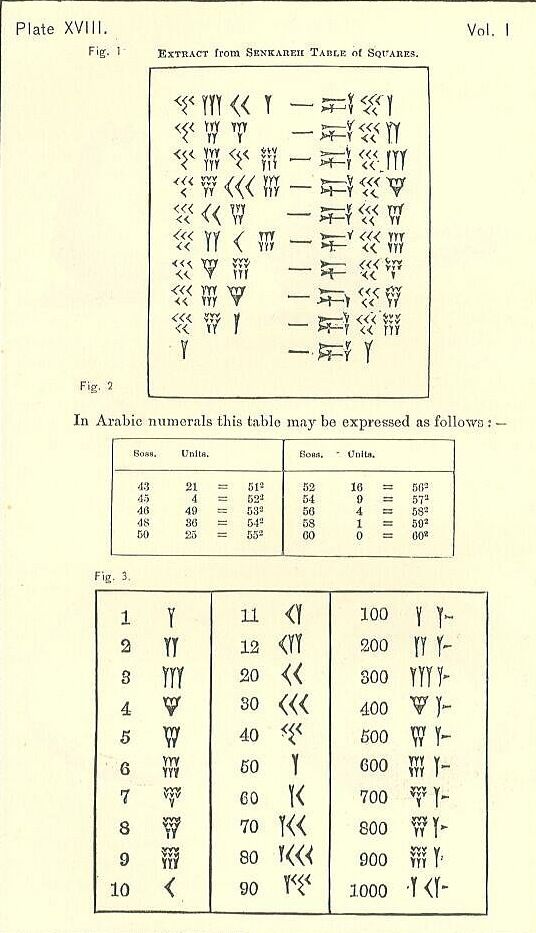
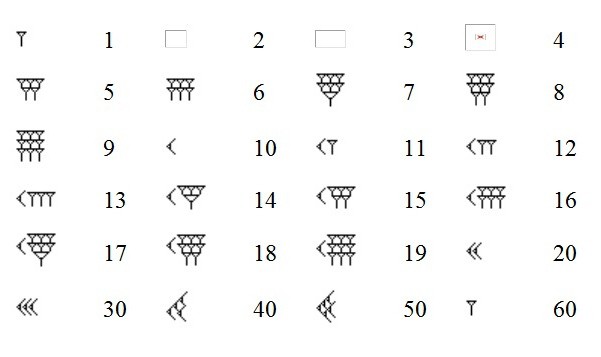
බැබිලෝනියානු ගණිතයේ භාවිතා කරන සංකේත සංඛ්යාව

මම කළ යුතු දේ නම්, මම සහ ත්රිකෝණය වැනි රේඛාවක් ලිවීමට ඉගෙන ගැනීමට කොතරම් පහසු නම්, ගණිතය ඉගෙන ගැනීමට පහසු වනු ඇතිදැයි සිතන්න. එය මූලිකවම මෙසපොතේමියාවේ සියලු පුරාණ ජනයා කළ යුතුව තිබුණද, මෙහිදී ඒවා වෙනස් කර, දිගු කිරීම, හැරීම වැනි ය.
ඒ සඳහා අපේ පෑන් සහ පැන්සල් හෝ කඩදාසි තිබුණේ නැහැ. ඔවුන් ලියූ දේ, මැටි මලක් නිසා, මූර්තිවල භාවිතා කරන උපකරණයකි. මෙම පැන්සලකට වඩා හැසිරවීමට ඉගෙනීමට පහසු හෝ පහසු වන්නේ එය වේගවත් කිරීමක් වන නමුත්, මේ දක්වා ඔවුන් දුරස්ථව දෙපාර්තමේන්තුවට ඉදිරියට යන අතර, ඉගෙන ගැනීමට මූලික සංකේත දෙකක් පමණක් ඇත.

කඳවුර 60

මීලඟ පියවර, සරල බවකින් යුක්තව හැඩයක් ලබා දෙයි. අපි Base 10, සංකේත දහයක් තිබීම නිසා පැහැදිලිව පෙනෙන සංකල්පයකි. ඇත්ත වශයෙන්ම අපට ඇත්ත වශයෙන්ම ඇත්තේ 20 ක් පමණි. එහෙත්, අප විසින් මැටි පුවරු පුළුස්සා මරා දැමීමට සහ පසුදා සතළිසක් සොයා ගැනීම සඳහා එම සූර්යයා සිට වැලි තබා වැලි තබා ගැනීම සඳහා ආරක්ෂිත පෑන් ආවරණ සහිත පාවහන් සැහැල්ලු කරමු. බැබිලෝනිවරුන් මෙම පදනම 10 යොදා ගත් නමුත් ඉන් කොටසක් පමණි. කොටසක් වශයෙන් ඔවුන් භාවිතා කළේ පාදම 60, මිනිත්තු, තත්පර සහ ත්රිකෝණයක හෝ රවුමක දී අප වටා සිටින එකම අංකයයි. ඔවුන් තාරකා විද්යාඥයින්ගේ දක්ෂතාවයන් නිසා ඒවායේ ප්රමාණය නිරීක්ෂණය කළ හැකි විය. පාදයේ 60 ද එය ගණනය කිරීම පහසු කරවන විවිධ ප්රයෝජනවත් සාධක ඇත. එහෙත් 60 වන පදනම ඉගෙන ගැනීමෙන් බිය ගැන්වීමය.

"බබිලෝනියට ගරු කිරීම" [ The Mathematical Gazette , Vol. ගණිතය ඉගැන්වීමේ දී ගණිතයේ ඉතිහාසය භාවිතා කිරීම (මාර්තු 1992), ලේඛක-ගුරුවරයෙකු වන නික් මැකිනෝන් පවසන පරිදි ඔහු බබිලෝනීය ගණිතය භාවිතා කරන්නේ වසර 13 ක් පුරා ඉගැන්වීමටය. බැබිලෝනියානු පද්ධතියේ පාදම 60 ට භාවිතා කරයි. එයින් අදහස් වන්නේ දශමස්ථානය වෙනුවට, එය ලිංගිකමය.

මෙම සරළකමේ අනුපාතය දැන් 1: 1 යි.

ස්ථානීය අංකනය

බබිලෝනීය සංඛ්යා පද්ධතිය සහ අපගේ දෙකම වටිනාකමක් ලබා දෙන තැනක් මත රඳා සිටිනවා. මෙම ක්රම දෙක එකිනෙකට වෙනස් වේ, ඔවුන්ගේ පද්ධතියට ශුන්යයක් නොතිබූ නිසාය. බබිලෝනියානු වමේ සිට දකුණට (ඉහළ සිට පහළට) ස්ථානගත ක්රමයක් මූලික මූලික ගණිතයේ පළමු රසය ඉගෙන ගැනීම සඳහා අපගේ 2-දිශා අක්ෂරය ඉගෙන ගැනීමට වඩා අපහසු නොවේ, දශාංශික සංඛ්යා අනුපිළිවෙල මතක තබා ගත යුතුය - දශමයෙන් සිට දශමයකින් , දස දහස් ගණනක්, අනෙක් පැත්තෙන් අනෙක් පැත්තෙන් අනෙක් පැත්තට වන්නට පුලුවන්, ඔන්ටෙත්ස් තීරුව, දසයෙන්, සියයෙන් එකක, දහස් ගණනක් වැනි ය.

ටයි පටිය තවමත් පවතී.
තවදුරටත් බබිලෝනීය පද්ධතියේ පිහිටීම්වලට මම පිවිසෙන්නෙමි. නමුත් මුලින්ම, ඉගෙනීමට වැදගත් වචන කිහිපයක් තිබේ.

බබිලෝනියානු අවුරුදු

අපි දශම සංඛ්යා භාවිතා කරමින් අවුරුදු යුගයන් ගැන කතා කරමු. අවුරුදු 10 ක්, අවුරුදු 100 ක් (දශක 10 ක්) හෝ 10X10 = අවුරුදු 10 ක් වර්ගයේ සහ අවුරුදු 1000 ට (ශත වර්ෂ 10 ක්) හෝ 10X100 = 10 වසරකට කුකුල් අවුරුදු දශකයක් අපට තිබෙනවා. මට වඩා උසස් පදයක් ගැන මම දන්නේ නැහැ. නමුත් ඒවා බබිලෝනිය පාවිච්චි කළ ඒකක නොවේ. නීල් මැකිනොන් බැබිලෝනිවරුන් විසින් භාවිතා කරන ලද යුගයන් සඳහා පමණක් නොව සර්න් හෙන්රි රෙලින්සන් (1810-1895) විසින් සෙන්ක්රේreh (ලාර්ෂා) ටැබ්ලට් එකක් ගැන සඳහන් කරයි.

1. සෝස්
2. ආර්
3. සාර් .

පාස්කු අවුරුදු 60 ක කාලයක් පුරා හැඳින්වේ. වසර 600 ක ඒකකය, හෝ එක් පාස්කු භාගයක් පමණ වේ. [බැබිලෝනියානු පද්ධතිය ලිංගිකව මරා දමන ලද අතර, එය දශම වශයෙන් දශම] සහ 3600 වසරක ඒකකයක් වන සාර්ක් ලෙස සැලකේ .
තවමත් ටයි-බ්රේකර්: ලතින් භාෂාවෙන් ලතින් භාෂාවෙන් කියුබත් හා කියුබේරී අවුරුදු නියමයන් ඉගෙන ගැනීමට පහසු නොවේ. එය කියුං කිරීම නොවන අතර, බබිලෝනියානු අක්ෂරවලින් පමණක් නොව, ගුණ කිරීම මගින් 10 ගුණයකින් යුක්ත වේ.
ඔයා සිතන්නේ කුමක් ද? බැබිලෝනියානු පාසැල් දරුවෙකු ලෙස ඉංග්රීසි භාෂාව කතා කරන පාසැලේ නවීන සිසුවෙකු ලෙස මූලික කරුණු ඉගෙනීම අසීරු විය හැකිද?

* ජෝර්ජ් රෙලින්සන් (1812-1902), හෙන්රිගේ සොහොයුරු, පුරාතන නැඟෙනහිර ලෝකයේ මහා රාජකීය සත්වයින්ගේ චතුරස්රාකාර සරල වගුවක් පෙන්වයි. බැබිලෝනියානු යුගයේ කාණ්ඩ මත පදනම්ව වගුව පෙනෙන්නේ තාරකා විද්යාවයි.

> සියළුම ඡායාරූපවලින් පෙනී යන්නේ 19 වන සියවසේ ජෝර්ජ් රෙලින්සන්ගේ පුරාණ නැගෙනහිර ලෝක ශ්රේෂ්ඨ රාජාණ්ඩුවයි .

05 සිට 05 දක්වා

බබිලෝනියේ ගණිත සංඛ්යා

කුකුළා වගුව http://www.gutenberg.org/files/16161/16161-h/16161-h.htm - මහා රාජාණ්ඩු හීන්, ජී. රාවින්සන්

අපි වෙනස් ක්රමයකින් හැදී වැඩුණු නිසා, බබිලෝනියානු සංඛ්යා අවුල් සහගතයි.
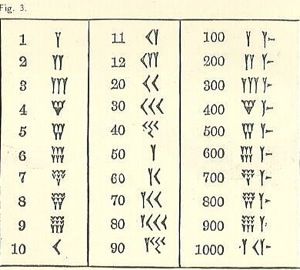
අඩුම තරමේ වමේ සිට ඉහළට වම් පැත්තෙන් දකුණට පහළින් ද අපේ අරාබි පද්ධතිය මෙන්, අනෙක් ඒවා නුසුදුසු බවක් පෙනේ. එක් එක් සංකේතය වන්නේ කන් හෝ Y හැඩැති ආකෘතියකි. අවාසනාවකට මෙන්, Y නියෝජනය වන්නේ 50 ක් පමණි. වෙනම සංකේත කිහිපයක් ඇත (සියල්ලම සාදා සහ රේඛාව මත පදනම්ව), නමුත් අනෙකුත් සියලු සංඛ්යාවන්ගෙන් ඒවා සෑදී ඇත.
ලිඛිත ස්වරූපය මතකයේ තබා ගන්න. රේඛා ඇඳීමට භාවිතා කරන මෙවලම නිසා සීමිත විවිධත්වයක් ඇත. කුරුල්ලේ කොටසක් ත්රිකෝණාකාර ස්වරූපයක් මුද්රණය කිරීමෙන් මැටි දිගේ උල් පිඩැල්ල අදින්න, ඇදගෙන යාමෙන් හෝ නොතිබිය හැකිය.
ඊතලයක් ලෙස විස්තර කර ඇති 10, ඇඳක් මෙන් දිස්වෙයි.
කුඩා 3s දක්වා දක්වා ඇති පේළි තුනක් (සමහර කෙටි ආවරණය සහිත ටයිල් සහිතව ලියන ලද) හෝ 10s (a 10 ලෙස ලියා ඇත) එකට එකට පටලවා ඇත. ඉහළ පේළිය පළමුව මුලින්ම පුරවා ඇත, දෙවනුව, පසුව තෙවනුව. ඊළඟ පිටුව බලන්න.
05 සිට 05 දක්වා

1 පේළිය, පේළි දෙකක් සහ පේළි 3 ක්

කුට්ටි වගුව. http://www.gutenberg.org/files/16161/16161-h/16161-h.htm - මහා රාජාණ්ඩු හීන්, ජී. රාවින්සන්

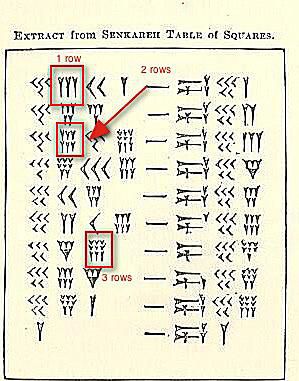
ඉහත උපමාවෙහි උද්දීපනය කළ උච්චාරණ සංඛ්යාවක කාණ්ඩ තුනක් ඇත.
දැන් අපි ඔවුන්ගේ වටිනාකම ගැන සැලකිල්ලක් නොදක්වුවත් එකී සංඛ්යාවෙන් 4 සිට 9 දක්වා ඕනෑම ස්ථානයක (හෝ ලිවීමට) ඔබ දකිනු ඇති ආකාරය නිරූපණය කර පෙන්වයි. තුන්දෙනා පේළියට යන්න. සතරවන, පස්වන හෝ හයවෙනි නම්, එය පහලයි. හත්වන, අටවෙනි හෝ නවවන නම් ඔබට තුන්වන පේළිය අවශ්ය වේ.
බැබිලෝනියානු අධිපතිකම සමඟ ක්රියාත්මක වන ගණනය කිරීම් පිළිබඳ උපදෙස් පහත දැක්වේ.
05 සිට 05 දක්වා

කුට්ටි වගුව

කුහර සංචලනයේ කුඩාව http://www.gutenberg.org/files/16161/16161-h/16161-h.htm - මහා රාජාණ්ඩු හීන්, ජී. රාවින්සන්

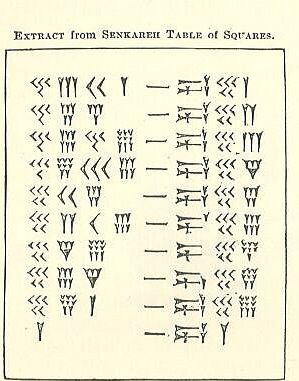
සීසර් ගැන ඔබ කියවා ඇති දේ වලින් - ඔබ මතක තබා ගත යුතු වනාහි වසර 60 ක් තිස්සේ බබිලෝනියානු, උල් පිඩැල්ල සහ අල්ෙපෝඩිං යන අක්ෂර සඳහා විස්තරාත්මක නමක් වන අතර, මෙම ගණනය කිරීම් සිදු කරන්නේ කෙසේදැයි සොයා බලන්න. ඩැඑෂ්-සමාන සලකුණෙහි එක පැත්ත වන්නේ අංකය වන අතර අනෙක චතුරාර්යය වේ. කණ්ඩායමක් ලෙස එය උත්සාහ කරන්න. ඔබට එය සොයාගත නොහැකි නම්, ඊළඟ පියවර බලන්න.
05 සිට 05 දක්වා

කුට්ටි වගුව විකේතනය කරන්නේ කෙසේද?

කුහරයේ කුහර සංචාලනයේ අරාබි පරිවර්තනය. http://www.gutenberg.org/files/16161/16161-h/16161-h.htm - මහා රාජාණ්ඩු හීන්, ජී. රාවින්සන්

ඔබට එය දැනගත හැකිද? එය අවස්ථාවක් දෙන්න.
...

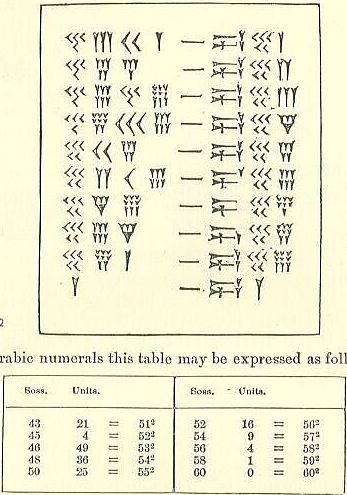
වම් පැත්තෙන් පැහැදිලි තීරු 4 ක් පසුව ඩැෂ්-සමාන ලකුණක් සහ දකුණු පස තීරු 3 ක් ඇත. වම් පැත්ත දෙස බැලූ විට, 1s තීරුවේ සමාන අගයක් වන්නේ "dash" (අභ්යන්තර තීරු) වලට ආසන්නතම තීරු දෙකයි. අනෙක් 2, පිටත තීරු 60 වැනි තීරුව ලෙස ගණන් ගනු ලැබේ.

                                රෝමානු සංඛ්‍යා                        

කොලසියමයෙහි LII (52) කොටසට ඇතුළුවන දොරටුව, සංඛ්‍යා තවමත් දර්ශනය වෙයි

පුරාතන රෝමයේ භාවිතා කෙරුණු සංඛ්‍යා ක්‍රමය වූ රෝමානු සංඛ්‍යා යනු, අගයයන් විදහා පෑමට ලතින් හෝඩියේ අකුරු වල සංයෝජනයන් භාවිතා කල ක්‍රමයකි. . 1 සිට 10 දක්වා සංඛ්‍යා, රෝමානු සංඛ්‍යා විසින් දක්වන්නේ පහත ලෙසිනි:

I, II, III, IV, V, VI, VII, VIII, IX, X.

රෝමානු සංඛ්‍යා ක්‍රමය, එට්‍රස්කානු සංඛ්‍යා වලට ඥාතිත්වයක් දක්වයි. රෝමානු අධිරාජ්‍යයෙහි අභාවයෙන් පසුව වුද රෝමානු සංඛ්‍යා භාවිතය දිගටම පැවතිණි. 14වන සියවසෙන් පසුව, රෝමානු සංඛ්‍යා වෙනුවට, වඩාත් පහසු හින්දු-අරාබි සංඛ්‍යා ආදේශ වීම ඇරඹිණි; කෙසේවෙතත් මෙම ක්‍රියාවලිය ක්‍රමයෙන් සිදුවූවක් වූ අතර, වර්තමානයේ වුවද සමහරක් සුළු නියැලුම්හී රෝමානු සංඛ්‍යා භාවිතය දක්නට ලැබේ.

රෝමානු සංඛ්‍යා කියැවීම[සංස්කරණය]

MMXX

"2020" රෝමානු සංඛ්‍යාවක් ලෙසින්

වර්තමානයේ භාවිතා කෙරෙන, රෝමානු සංඛ්‍යා පදනම්ව ඇත්තේ සංකේත හතක් මතය:^[1]

සංකේතය	අගය
I	1
V	5
X	10
L	50
C	100
D	500
M	1,000

සංඛ්‍යා සදනු ලබන්නේ සංකේත සංයෝග කිරීමෙන් සහ අගයයන් එකතු කිරීමෙනි. මෙලෙස, II යනු එකේ ඒවා දෙකකි, එනම් 2 වෙන අතර, XIII යනු දහයේ එකක් සහ එකේ ඒවා තුනකි, එනම් 13 වෙයි. මෙම ක්‍රමයෙහි ශුන්‍ය නොමැති අතර, එබැවින් 207, නිදසුනක් ලෙසින්, CCVII වන්නේ, සියයේ ඒවා දෙකක්, පහේ එකක් හා එකේ ඒවා දෙකක් සඳහා සංකේත භාවිතයෙනි. 1066 යනු MLXVI, එක් දහස්, පනහ සහ දහය, පහක් සහ එකක් වෙයි.

                   පුරාණ ඊජිප්තුවේ ගණිතය                        

පුරාණ ඊජිප්තු වැසියන් විසින් ඔවුන්ගේ ගණිත දැනුම වර්ධනය කරගත්තේ ඔවුන්ට සැබෑවටම ඇති ප්‍රශ්න සඳහා ප්‍රායෝගික විසඳුම් ලබා ගැනීම සඳහාය. නයිල් නදියේ වසරකට ගලන ජල ධාරිතාව, භූමි ප්‍රමාණය, මුදල් එකතු කිරීම හා බදු අය කිරීම ආදිය සඳහා ඔවුන් ගණිත දැනුම භාවිතා කරන ලදි.

 ගොඩනැගිලි කර්මාන්තයේදී ජ්‍යාමිතිය පිලිබඳ දැනුම ඔවුන්ට බෙහෙවින් උවමනා විය. කඩ හිමියන් හා කෑම උයන්නන් සරල ගණිත ක්‍රමය භාවිතා කල අතර පූජකවරු, බදු එකතු කරන්නන්, ගොඩනැගිලි සාදන්නන් ආදිය සංකීර්ණ ගණිත ක්‍රම භාවිතා කලහ.

 පුරාණ ඊජිප්තු වැසියන් ඉලක්කම් සදහා භාවිතා කලේ එක , දහය හා දහයේ ගුණාකාර [උදා. 100, 1000 වැනි] ය. ඉලක්කම් යැයි කීවද භාවිතා කලේ ඒවටම වෙන්වූ සංකේත ය. සංඛ්‍යාවක් ලිවීමේදී එකම සංකේතය කිහිප වාරයක් යොදයි. රෝම ඉලක්කම් ක්‍රමයට මෙය තරමක් සමාන වේ.

 පුරාණ ඊජිප්තුව තුල ගණිතය පිලිඹඳ දැන ගැනීමට ඔවුන් තැබූ සටහන් බොහෝ ප්‍රයෝජවත් වේ. සමහර පැපිරස් පත්‍ර වල භාග සුළු කරන ආකාරය පිලිබඳ වගු, විවිධ ස්කන්ධ හා පරිමාණ පරිවර්තනය පිලිබඳව සදහන් වේ.

රින්ඩේ පැපිරස් පත්‍රය යනු අඩි 15ක් පමණ දිග හකුලන පැපිරස් පත්‍රයකි. මෙය ලියා ඇත්තේ ක්‍රි.පූ. 1660 දීය. මෙය තුල ගණිත ප්‍රශ්න හා ඒවාට පිලිතුර බොහොමයක් ඇතුලත් වේ. මෙය පුරාණ ඊජිප්තුව තුල දියුණු ගණිත ක්‍රම, සමීකරණ මගින් ගැටලු විසදීම ආදිය ගැන මොනවට සක්ෂි දරයි. ඔවුන්ට ඉන්ජිනේරු විද්‍යාව පිලිබඳවත් හොද දැනුමකින් තිබීය.

 මොවුන් එකතු කිරීම, අඩු කිරීම, බෙදීම, ගුණකිරීම පිලිබදව දැන සිටියහ. එමෙන්ම වර්ගමූලය, ත්‍රිකෝණයක හා වෘත්තයක වර්ගඵලය සෙවීමද දැන සිටියහ. පයිතගරස් මූලදර්මයේ මූලික සිද්ධන්තද දැන සිටියහ.

 ඊජිප්තුවන් පයිතගරස්, ඉයුක්ලිඩ් හා ප්ලේටෝගෙන් ජ්‍යාමිතිය තවදුරටත් ඉගෙන ගත්තේය. 19 වන ශතවර්ෂයේ Saqqara නැමැති පැරණි ඊජිප්තියානු සුසාන භූමියේ සිට සොයාගත් ක්‍රි.පූ. 1300 - 1200 කාලයට අයත් වන බර්ලින් පැපිරසයේ පහත සදහන් ගණිත ප්‍රශ්නය නිරූපනය වේ.

සමචතුරස්‍ර බිම් කැබලි දෙකකින් වර්ග ඒකක 100ක වර්ගඵලයක් නිර්මාණය කිරීමට අවශ්‍යව ඇත. එක් සමචතුරස්‍රයක දිග අනෙක් සමචතුරස්‍රයේ දිග මෙන් 1/2 + 1/4 ක් වේ. සමචතුරස්‍ර දෙකේ එක් පැත්තක දිග වන්නේ කුමන අගයක්ද යන්න විසඳීමට උත්සහ දරා ඇත.

මෙම ප්‍රශ්නය පහත දැක්වෙන සමීකරණය ආශ්‍රයෙන් දැක්විය හැක. X^2 + Y^2 = 100 X = 3Y/4 වර්ගජ සමීකරණයක් විසඳීමට තැත් කල ලොව පලමු උත්සහය ලෙස මෙය සැලකේ. මෙලෙස වර්ගජ සමීකරණ ජීවිත කතාවේ මුල් පියවර පුරාණ ඊජිප්තුවන්ට හිමි විය.

වෘත්තයක පරිධිය එහි විශ්කම්භයෙන් බෙදූ විට ලැබෙන්නේ 3.14 ට ආසන්න අගයකි. 22/7 මෙම අගයට බොහෝ දුරට සමාන වේ. මෙයට අපි ෆයි යැයි කියති. පිරමීඩයකත් පතුලේ වට ප්‍රමාණය එහි උස මෙන් දෙගුණයකින් බෙදුව විට ලැබෙන අගය 3.14 වේ.

මූලාශ්‍ර:

1) http://www.egyptominia.com/2017/04/physics-of-pharaohs_36.html?m=1

2) http://www.egyptominia.com/2017/05/mathematics-in-ancient-egypt.html?m=1

3) https://discoveringegypt.com/egyptian-hieroglyphic-writing/egyptian-mathematics-numbers-hieroglyphs/

සංඛ්යා ඉතිහාසය. සැබෑ සංඛ්යා සංවර්ධන ඉතිහාසයේ

නූතන ශිෂ්ඨාචාරය සංඛ්යා නැතිව උපකල්පනය හුදෙක් නොහැකි ය. අපි සෑම දිනකම ඔවුන් මුහුණ, අපි ඔවුන්ට දුසිම් ගනනක්, පරිගණක මගින් ක්රියා සිය දහස් ගණනක් කරන්න. සංඛ්යා ඉතිහාසය අප ගැන උනන්දුවක් නැති බව එය එසේ භාවිතා කර ඇති අතර, එය බොහෝ සරලව හිතුවේ නැහැ ඇත. එහෙත් පසුගිය අනුදැනුමකින් තොරව වත්මන් වටහා කළ හැකි අතර, එම නිසා ඔබ හැම විටම සම්භවය තේරුම් ගැනීමට උත්සාහ කළ යුතුය.

ඒ නිසා අංක ඉතිහාසය කුමක්ද? මිනිසෙකු සිය නිර්මාණය කිරීමට පැමිණි විට ඔවුන් පෙනී? අපට ඒ ගැන දැනුම් දෙන්න!

සංවර්ධන

ගණිතයේ දී, තවත් වැදගත් අංගයක් පවතී. මෙම හමුවේ වුවද, සංකල්පයක් ලෙස සංඛ්යාව අවුරුදු දහස් ගණනක් පුරා පරිණාමය වී ඇත ලොව පුරා විද්යාඥයන් සිත් එය සංජානනය කිරීමට ආකාරය පිළිබඳ තවමත් එකඟ නැහැ සමාන නොවේ.
දැඩි මෙම සංකල්පය ඉස්මතු ඉල්ලා ඇති විනය පළමු භාවිතය, කෘෂිකාර්මික, ඉදිකිරීම්, හා තාරකා නිරීක්ෂණ සමග සම්බන්ධ වී ඇත. අනෙක් අතට, අහස අධ්යයනය හා සියලු මිනුම් වර්ගීකරණය කරන තොරව එය ඕනෑම රාජ්ය සංවර්ධනය විය නොහැක්කේ නාවික හා ජාත්යන්තර වෙළෙඳ සංවර්ධනය, ඉතා වැදගත් වේ.

ටිකක් දර්ශනය

වඩාත්ම ආදි සංඛ්යාලේඛන පවා ශත වර්ෂ ගණනාවක් සිදු කළ හා පොදු මතකයට ගෙන එන ලදී. ඔවුන්ගෙන් බොහෝ වචන හෝ තනි තනි ලිපි නිර්මාණ අරභයා ප්රතිඵලයක් ලෙස ස්ථාපිත කරන ලදී. සුප්රසිද්ධ පයිතගරස් සංඛ්යා සමස්ත විශ්වය නිර්මාණය වන සිට එසේ අභිරහස්, ඒකට ද්රව්යයක් බව ඒ මහතා කියයි. පොදුවේ ගත් කල, විද්යාව නූතන සංකල්ප අනුව, ඔහු බොහෝ දුරට හරි.
චීන සංඛ්යාව (මේ දවස දක්වා ආරක්ෂා වී ඇති) පුළුල් කාණ්ඩ දෙකකට බෙදා වෙන්:

• අමුතු හෝ යැං. පුරාණ චීන දර්ශනය තුල ඔවුන් ස්වර්ගයට හා auspiciousness සංකේතවත් කරයි.
• ඒ අනුව, පවා (යින්). මෙම සංකල්පය පොළොව හා අස්ථාවරත්වය සංකේතවත් කරයි.

අතීතයේ සිට ම ...

ඔබ බොහෝ විට මේ වන විටත් අංක ඉතිහාසය පුරාණයේ කාලයේ සිට දුවනවා බලමින් ආරම්භ වන අනුමාන කරනවා. එම අවස්ථාවේ දී, අභිරහස් චරිත අපේ ලෝකය ගණිතඥයන් ඉතිහාසයේ ප්රථම බවට පත් වූ පූජකයන්, පමණක් වරප්රසාදිත අවබෝධයක් ලබා ගත හැකි විය.
මානව විද්යාඥයන් හා පුරාවිද්යාඥයන් දැඩිව පුද්ගලයෙකු ගල් යුගය දැනටමත් සලකා බැලිය හැකි බව තහවුරු කර ඇත. මුලින්ම, පළමු අංකය ඇඟිලි හා ඇඟිලි සුවිශේෂී ප්රමාණය නිරූපණය කෙරේ. අප ලබා ගන්නා පියවර ගණන් කිරීමට ඔවුන් පාවිච්චි සතුරන් ... මුලින්ම, ජනතාව සරල අංක කිහිපයක් පමණක් අවශ්ය, නමුත් සමාජයේ සංවර්ධනය වඩ වඩාත් සංකීර්න පද්ධති අවශ්ය වේ. මෙම ගණිත වසරේදී තමාගේම සංවර්ධනය කිරීමට හේතු, පමණක් නොව, බුද්ධිමය වැඩ මානසික ආතතිය අවශ්ය පරිදි, සාමාන්යයෙන් මානව ශිෂ්ටාචාරයේ සංවර්ධනය කිරීමට දායක පමණක් නොවේ.
ඒ නිසා පැන නැගීම හා සංවර්ධනය පිළිබඳ කතාව සමග ආබද්ධ මනස වැඩි දියුණු කිරීම සහ ස්වයං-වර්ධනය කිරීමට අපේ මුතුන් මිත්තන් ආශාව සමඟ සම්බන්ධ වී පවතී. වඩා ඔවුන් තාරකා, (පවා ප්රාථමික මට්ටමේ) ගණිතමය ක්රමානුකූලභාවය ගැන වැඩි වැඩියෙන් කල්පනා ලෝකයේ ඔවුන් වටා ප්රඥාවන්ත බවට පත් බැලුවා.

සංඛ්යාව ප්රතිභාන සංකල්පය

පළමු කේවලකට විය විගස ජනතාව ඔහුට ඉදිරිපත් කරන නිෂ්පාදන සඳහා එම අගයන් සමග සමහර වස්තූන් සංඛ්යාව සංසන්දනය කිරීමට පාඩමක් ආරම්භ කළා. "වඩා අඩු", "සම", "වඩා" සංකල්ප "තරම්." දැනුම ඉක්මනින් සංකීර්ණ බවට පත් වෙයි, සහ නිසා ඉක්මනින් ගණනය පද්ධතියක් සඳහා අවශ්ය විය.
එය යථාර්ථය අංක ඉතිහාසය සාධාරණ පුද්ගලයෙකු පළමු පෙනුම සමග ආරම්භ කළ බව මතක තබා ගත යුතුය. තවමත් පවා සරල ගණිත ගැන ඉඟියක් නැති, මිනිසුන්, සතුන්, වස්තු සංඛ්යාව සංසන්දනය කරන ආකාරය ඔහු අවිවාදයෙන්ම පිළිගැනීමට දැන සිටියේය. නමුත් ඒ අමුතු දෙයක් විය: ඕනෑම වස්තුවක් ස්පර්ශ කළ හැකි, සහ ඔවුන්ගෙන් අංකය සහ ගොඩක් පහසුවෙන් නවනු නැත.
මෙම එකම භාණ්ඩ ගුණ විස්තර කරන සංඛ්යා පවතී, නමුත් ස්පර්ශ කිරීමට හෝ ඒවා නොහැකි විය සන්සන්දනය කිරීම. මෙම දේපල ඔවුන් අංක ඉන්ද්රජාලික, ආශ්චර්යමත් ගුණාත්මක ආරෝපනය, බිය ජනතාව තුඩු දී තිබේ.

කල්පිත සමහර සාක්ෂි

මුලින් තුනක් පමණක් සෙනඟ "එක", "දෙක" සහ "බොහෝ" යන සංකල්පය භාවිතා කර ඇත බව දීර්ඝ කාලයක් පුරා විද්යාඥයින් උපකල්පනය කර ඇත. , ඒක වචන ද්විත්ව හා බහු වචන: මෙම කල්පිතය සිනහ බොහෝ පුරාණ භාෂා (උදාහරණයක් ග්රීක, දී) හරියටම තුන් ආකාර බව, ඒ මගින් සනාථ වෙයි. ටික දවසකට පස්සේ, මිනිස්සු හඳුනාගැනීමට, උදාහරණයක් ලෙස, මී හරක්, දෙක, තුන, ඉගෙනගත්තා. ආරම්භයේ දී, ලකුණු වස්තූන් යම් විශේෂිත කට්ටලයක් සමඟ සම්බන්ධ වී ඇත.
"එක" සහ "දෙක", සහ ඒකාබද්ධ කොට ජනතාවට ලැබුණු අනෙකුත් සියලු සංඛ්යා: මෑතක් වන තුරු, දේශීය ඕස්ට්රේලියානු හා Polynesians දෙකක් පමණක් ඉලක්කම් විය. උදාහරණයක් ලෙස, තුන් සංඛ්යාව - දෙකක් හා එක් සිව් - දෙකක් හා එකට. එය සැලකිය යුතු තරම් සමාන වේ ද්විමය ක්රමය , දැන් පරිගණක තාක්ෂණය භාවිතා කරන ගණනය! කෙසේ වෙතත්, ඉගෙන ගැනීමට බල ඒ කාලයේ කටුක ජීවිතය, සහ ඉක්මනින් විසින් එසේ ප්රාථමික ගණිතමය විද්යාව බවට පත් විය.

බබිලෝනියේ හා මෙසපොතේමියාවේ

දී පුරාණ බබිලෝනියේ මෙම රාජ්ය කිසිදු ගණනය කිරීම් ඉදි කිරීමට නොහැකි වී ඇති බව දැවැන්ත, අතිශයින් සංකීර්ණ ව්යුහ නිර්මාණය කිරීමට නිසා ගණිතය, විශේෂයෙන් ම දියුණු කරන ලදී. නියමාකාර තරම්, නමුත් බැබිලෝනියානුවන්, වචනයේ පුළුල්ම අර්ථයෙන් අංකය පිළිබඳ සංකල්පය ඉතිහාසය ඔවුන් සමඟ හරියටම ආරම්භ ඒ නිසා, එම සංඛ්යා විශේෂ සංත්රාසයට පෝෂණය කළේ නැත.
බබිලෝනිය වස්තූන්, මිනිසුන් හෝ සතුන් උපරිම සංඛ්යාව චරිත අවම මාලාවක් වාර්තා හැකි බව ඔහුගේ සියලු සමකාලීනයන් ආරක්ෂා කළා. ඔවුන් ස්ථානීය පද්ධතිය සංඛ්යාත්මක සන්දර්භය තුළ වෙනස් තනතුරු හොබවා, එම සංඛ්යා ලේඛනවලට වෙනස් සංඛ්යාත්මක අගය ඇඟවෙන, පළමු වරට හඳුන්වා දෙන ලදී.
මීට අමතරව, ගණනය ඔවුන්ගේ පද්ධතිය ලබා ගත් ණය විද්යාඥයන් උපකල්පනය ලෙස බබිලෝනිය වන sexagesimal මිනුම් ක්රමය මත පදනම් වූ, සුමේරියානු ශිෂ්ටාචාරය. හිතන්න, නැවතුම් සංකල්පය මෙම ප්රදේශයේ ඉතිහාසය නමුත් කරන්න එපා. අපි තවමත් වට මිනුම් සන්දර්භය තුළ 60 විනාඩි, තත්පර 60 ක්, අංශක 360 සංකල්පය භාවිතා කරන්න.

පයිතගරස් බලාපොරොත්තුවෙන්

, බබිලෝනියේ ඉපැරණි ලියන්නන් දැනටමත් ත්රිකෝණ පිළිබඳ ගුණ ඉතා ප්රසිද්ධය. මීට අමතරව, ඔවුන් සීමාව අකුරු පිරමීඩයේ පරිමාව ගණනය සිදු කළා. අද එය, පරිමේය සංඛ්යා සංවර්ධනයේ ඉතිහාසය හරියටම ඒ කාලය මූලාරම්භය බව කවුරුත් හොඳින් දන්නා කාරණයකි: මෙසපොතේමියාවේ සහ බබිලෝනියේ ගණිත ක්රියාකාරීව භාග භාවිතා, නමුත් පවා unknowns තුනක් දක්වා සමග, ඔවුන්ගේ ප්රශ්නය විසඳා ගැනීමට උදව් විය හැකි එකම නැත!
පසුගිය කාලය තුළ දී, නවීන ගණිත ඔවුන්ගේ පැරණි පූර්වගාමීන් වර්ග, නමුත් කැට මූල පවා පමණක් නොව මිරිකා ගැනීම සාර්ථක බව ගැන පුදුම වූහ. ඔවුන් ද දළ වශයෙන් තුනක් දක්වා අඩු යයි වරදවා වටහා, Pi ඇති නිර්වචනය සමීප විය. එය මිසර වඩා බෙහෙවින් වඩාත් නිවැරදිව (3.16) වටිනාකම ගණනය කිරීම සඳහා හැකි වූ බව සඳහන් කළ යුතු ය.

ස්වාභාවික සංඛ්යා

කිසිදු අඩු පුරාණ ස්වභාවික අංකය සංවර්ධනය ඉතිහාසයයි. එය දැන් ඔහුගේ ලේඛන මෙම කාලීන පළමු භාවිතය රෝමානු විද්වතෙක් බෝතියස් බව (480-524 gg.) විශ්වාස කෙරේ, නමුත් Gerazy එතුමා Nicomachus සංඛ්යා ස්වභාවික, ස්වභාවික මාලාවක් මත, සිය ලිපි ලේඛන දී ලියූ බොහෝ කලකට පෙර.
කෙසේ වෙතත්, කාලීන "ස්වාභාවික අංකය" යන නූතන අර්ථයෙන් පමණක් D'Alembert (1717-1783 gg.) භාවිතා කර ඇත. නමුත් අපි තර්ක නොකළ යුතුය: ඔවුන් සමඟ ආරම්භ අධ්යයනය ම කියයි. ඇත්තෙන්ම, ස්වාභාවික, අංක 1, 2, 3, 4 වන ...
ඔවුන්ගේ පෙනුම සමග, අද අප දන්නා ඒවා වන ස්වරූපයෙන් ගණිතය හා වීජ ගණිතය ඉස්මතු දෙසට වන වැදගත් පියවරක් විය. නූතන ගණිත විශ්වාසයකින් යුතුව ස්වාභාවික සංඛ්යා අනන්ත මාලාවේ කතා කරන්න. ඇත්ත වශයෙන්ම, අතීතයේ දී, ජනතාව ඒ ගැන දැන සිටියේ නැත. "අඳුර", "සේනාංකය", "කට්ටලයක්" ද, එසේ මත යන වචනය මගින් වන ජනතාව හුදෙක් හිතාගන්න බෑ මුදල කොපමණද. මාර්ග සංඛ්යාව ඉතිහාසය ඉතා ඈත අතීතයේ එම නිසා ...

සකසන්න න්යාය

පළමුව, ස්වාභාවික සංඛ්යා ඉතා කෙටි විය. නමුත් ප්රසිද්ධ ආකිමිඩිස් I ෙකොටස: (III. ක්රි.පූ. ඊ) මෙම සංකල්පය ව්යාප්ත කිරීමට සමත් විය. එය මෙම අගනා විද්යාඥ ඔහුගේ සමකාලීනයන් බොහෝ විට සඳහන් කළ සේවය "යන වැලි Reckoner," ලීවේ "වැලි ඇට ගණනය." ඔහු නිවැරදිව න්යායිකව විෂ්කම්භය 15.000.000.000.000 කිලෝමීටර් සහිත ගෝලයක් සමස්ත පරිමාව අයිති විය හැකි ඉතා කුඩා අංශු, සංඛ්යාව ගණනය.
ආකිමිඩිස් ග්රීකයන් අංකය 10.000.000 දහසකුත් ළඟා කළමනාකරණය පෙර. දහසකුත්, කෙසේ වෙතත්, ඔවුන් සංඛ්යාව 10 000. පිහිටි ඉතා නම "අපරිමිත", "ඇදහිය නොහැකි තරම් විශාල" රුසියානු මාධ්යයක් බවට පරිවර්තනය කරන ලද ග්රීක "Miros", පැමිණෙන්නේ නම්. ආකිමිඩිස් ද ඉදිරියට ගොස්: ඔහු එහි ගනන් පසුව තම, කතෘගේ ගණනය පද්ධතිය නිර්මාණය කිරීම සඳහා ඔහු නායකත්වය දුන් 'දහසක්ද ක වර දහසක්ද "යන වචනය භාවිතා කිරීම ආරම්භ විය.
විද්යාඥයෙකු විස්තර හැකි උපරිම වටිනාකම, බිංදු 80.000.000.000.000.000 අඩංගු වේ. ඔබ දීර්ඝ කඩදාසි පටි මත මෙම සංඛ්යාව මුද්රණය නම්, එය මිලියන දෙකකට වඩා ගුණයක් සමකයේ දී ලොව වට හැකි ය.
මේ අනුව, සියලු ම ධන නිඛිල සඳහා ප්රධාන කාර්යයන් දෙකක් තිබේ:

• ඔවුන් ඕනෑම භාණ්ඩ ප්රමාණය කල හැක.
• ඔවුන්ගේ උදව් සමග සංඛ්යාව මාලාවක් වස්තු ගුණාංග විස්තර කරන්න.

reals

නමුත් සංවර්ධනයේ ඉතිහාසය ගැන මොකද , තාත්වික සංඛ්යා? සියලු පසු, ගණිතය, ඔවුන් කිසිදු අඩු වැදගත් ස්ථානයක් හිමි! පළමුව, මතක refresh. සැබෑ නම සාධනීය, සෘණ, සහ ශුන්ය විය හැක. ඔවුන් ගොඩක් තර්කානුකූල හා අහේතුක වෙන් කරනු ලැබේ.
ඔබ හොඳින් ලිපිය කියවන්න නම්, ඔබ, තාත්වික සංඛ්යා සංවර්ධන ඉතිහාසයේ මානව වර්ගයාගේ උදාවත් සමග ආරම්භ වන බව අනුමාන විය හැකිය. පළමු වරට (අඩු හෝ වැඩි විශ්වාසදායක තොරතුරු) සඳහා ශුන්ය සංකල්පය ක්රිස්තුස් පසු 876 වසරට සකස්, හා ඉන්දියාව හඳුන්වා බැවින්, ඔබ අතරමැදි ලෙස මෙම දිනය නිමිත්තෙන් හැක.
සෘණ අගයන් සඳහා පරිදි, පළමු වරට ක්රි.ව තුන්වන සියවසේ දී ඉමහත් ආලෝකයක් (ග්රීසිය) ඔවුන් විස්තර, නමුත් "නීතිගත", ඔවුන් පමණක් ඉන්දියාවේ, පාහේ එකවර "ශුන්ය" සංකල්පය සමග වූහ.
එය ගණිත වන අංක ඉතිහාසය බොහෝ විට පැහැදිලි වන ගණනය කිරීම් හේතුවෙන් පැරණි ඊජිප්තු පවතී ඔවුන් අවශ්ය බව මතක තබා ගත යුතුය. මෙන්න පමණක් ඔවුන්, "නොහැකි" සහ "යථාර්ථවාදී නොවන" ලෙස සලකන ලද ඉඳහිට අතරමැදි අගයන් ලෙස භාවිතා වුවත් අවස්ථාවේ ය.

පරිමේය සංඛ්යා

තාර්කික අංකය අල්පයක් බව ඔබට මතක ඇති. එය භාවිතා යනු පූර්ණ සංඛ්යාවකි numerator ස්වරූපයෙන්, සහ හරය තුළ ස්වාභාවික සංඛ්යා ලෙස ක්රියා කරයි. විටෙක මෙම සංකල්පය පළමු වරට මතු වී තිබේ, නමුත් ඔවුන් ක්රියාකාරීව වූ ක්රි.පූ දහස් ගණනක් වසර දැනටමත් සුමේරියන්වරුන් භාවිතා අපි දන්නේ නැහැ. ඔවුන්ගේ ආදර්ශය ග්රීකයන්ට හා මිසර වැසියන් විසින් අනුගමනය කරන ලදී.

සංකීර්ණ සංඛ්යා

නමුත් ඔවුන් සාපේක්ෂව මෑතකදී ලබා ඇති, වහාම ඝන සමීකරණය මුල් ගණනය කිරීම සඳහා ක්රම හඳුනාගෙන. මම දහසය වෙනි සියවසේ මුල ගැන මේ ඉතාලි කතා බොරු ෆොන්ටානා Tartaglia (1499-1557 gg.) කළා. එවිට ඔහු ප්රශ්න විවිධ ආකාරයේ විසඳීමට සෑම විටම එකම තාත්වික සංඛ්යා භාවිතා කිරීමට නොලැබෙන බව.
මෙම අමුතු සංසිද්ධිය පැහැදිලි කිරීමට පමණක් 1572 දී විය. එය රෆායෙල් Bombelli හැකි බවට, සංකීර්ණ සංඛ්යා සංවර්ධනය පිළිබඳ කතාව ආරම්භ වන සිට. නමුත් එකම 19 වන සියවසේ දී "quack පටබැඳීම්" ලෙස සලකනු දීර්ඝ කාලයක් තිස්සේ ඔහුගේ ප්රතිඵල, මහා ගණිතඥ කාල් ෆෙඩ්රික් Gauss ඔහුගේ ඈත පූර්වගාමියා හරියටම හරි බව ඔප්පු විය.